Percorsi ad alta densità cognitiva
il sito è in costruzione non tutti i contenuti sono disponibili
I percorsi ad alta densità cognitiva consentono un’esperienza cognitiva intensa, in un tempo breve, molto significativa ed altamente efficace.
Sono molto utili per la comprensione, lo sviluppo, il ripasso, il rinforzo e il recupero.
Essi usano idee e materiali, sia fisici che software e sono improntati ad un certo stile nel fare: puntare alla scoperta e stimolare capacità di pensiero produttive più che riproduttive. Inoltre sono divertenti e costruiscono una concezione positiva della matematica.
Sono applicabili in qualsiasi contesto:
in ogni classe e con ogni bambino, sia per chi presenta difficoltà, che per chi non ne presenta affatto;
nelle pluriclassi perché consentono attività simultanea differenziata e personalizzata;
in tutti quei casi in cui la presenza irregolare o a singhiozzo causa un apprendimento frammentario come ad esempio nelle zone ad alto rischio di dispersione scolastica;
in tutti i casi di emergenza educativa ...
Solo definizioni? Meglio di no
Tracciare con il nastro questo disegno in scala sul pavimento è un problema
Ma a cosa serve il filo e il gesso? Scopriamo raggio, diametro, circonferenza
Ora è facile tracciare anche gli altri cerchi
Il problema è risolto
Ora le definizioni hanno un senso
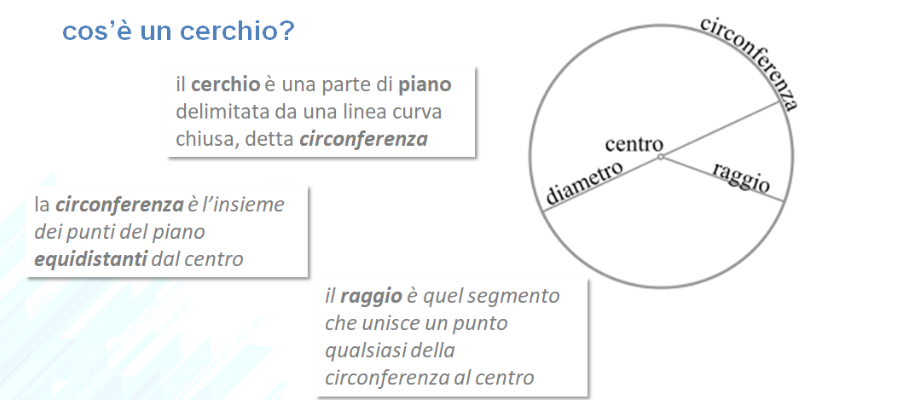
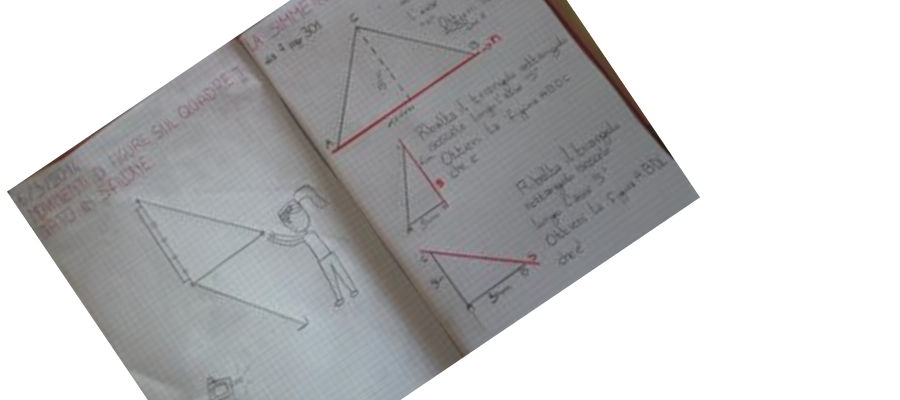
geometria in palestra
La geometria si può apprendere in vari modi, ma il modo migliore è sempre quello di sperimentarla, ad esempio cimentandosi in un vero problema. Così bastano un pavimento tipo quello della palestra, dove non mattonelle per fare da riferimento e semplici oggetti come un filo, un gesso, una squadra, un metro … e con un po’ di fantasia si costruisce un ambiente di apprendimento fantastico, dove fare geometria, fisicamente, e capirne i termini diventa interessante e divertente.
1/14 non dobbiamo partire da qui, dobbiamo arrivare qui solo dopo avere capito
> 2/14 possiamo partire da qui o da un gruppo di cartellini da riordinare
3/14 cartellini da ordinare
4/14 possiamo mettere lo zero qui
5/14 poi un numero alla volta possiamo completare
6/14 poi possiamo giocare ... che numeri mancano?
7/14 qui qualcosa non funziona ... sai trovare l'errore?
8/14 possiamo anche partire dalla fine e ordinare i numeri a ritroso
9/14 sai completare la sequenza?
10/14 se qui mettiamo il numero 8, quali numeri andranno dopo? E prima?
11/14 sai popolare la linea?
12/14 proviamo a partire anche così
13/14 tutto si costruisce e si fa con i bambini intorno per una linea costruita e camminata
14/14 poi si appende al muro e anche li ci si lavora
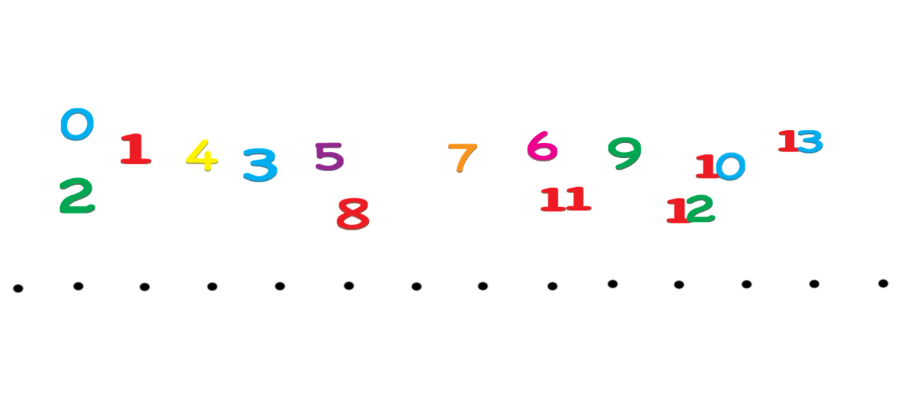
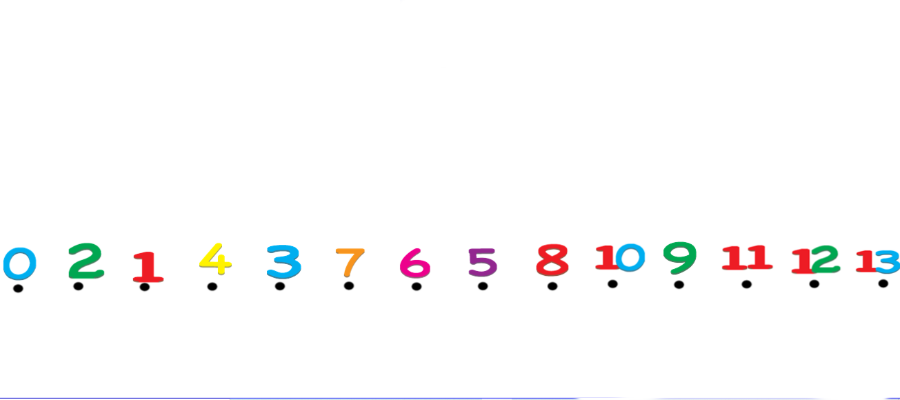
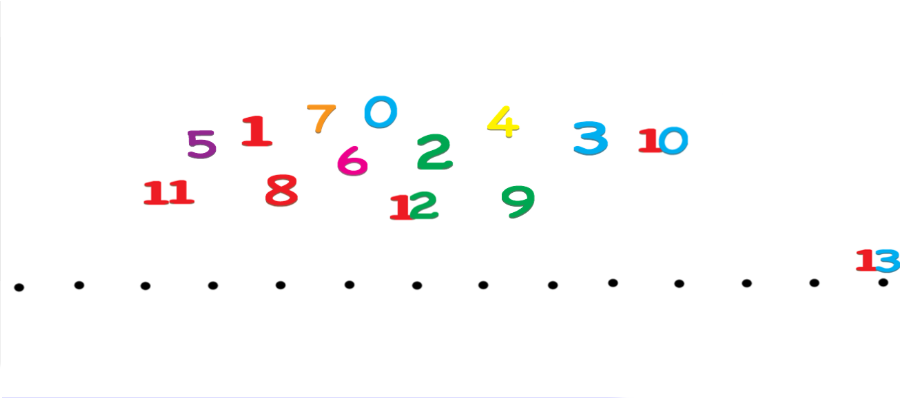
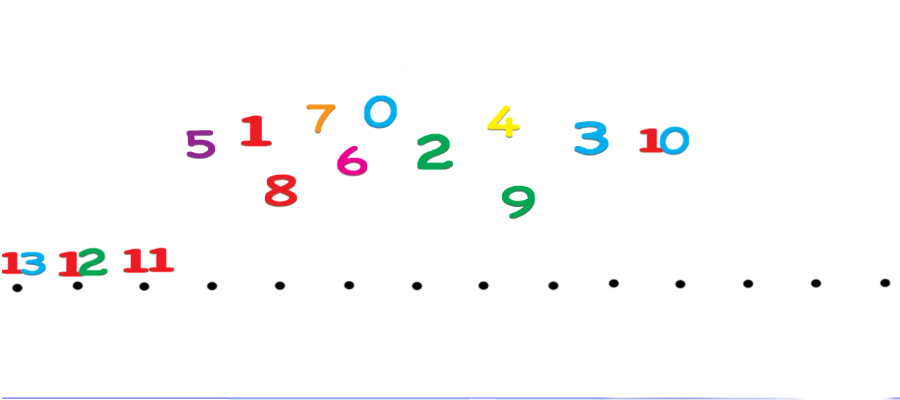
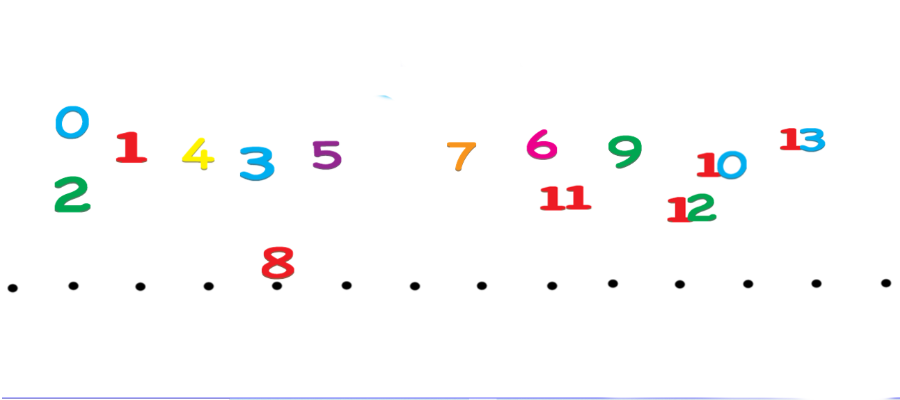
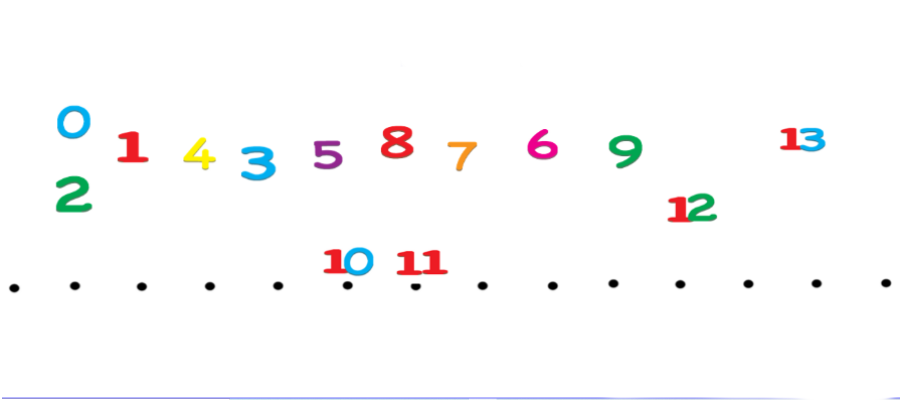
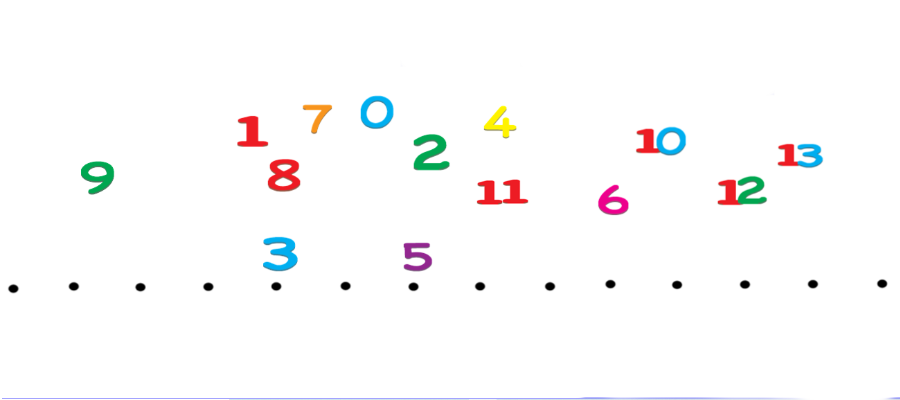
numeri in linea
I numeri si possono mettere in linea. Lo sappiamo. Ma è possibile costruire una linea che faccia pensare, capire e divertire? La linea dei numeri è uno strumento molto usato e molto utile. Se costruita, assieme ai bambini, in un certo modo, consente di capire come funzionano i numeri e di svolgere molte attività, oltre al semplice andare avanti e indietro, che stimolano riflessione, ragionamento, comprensione e risultano anche molto divertenti.
1/10 osserviamo due modi diversi di registrare la quantità centoundici
2/10 centoundici è composto da cento, dieci e uno
3/10 i sistemi di numerazione come ad esempio quello egizio usavano tre segni diversi
4/10 noi usiamo lo stesso segno sia per arppresentare cento che dieci che uno
5/10 osserviamo la differenza nella rappresentazione
6/10 cosa possiamo capire da questa osservazione?
7/10 Che nei sistemi antichi i segni hanno valore in sé mentre nel nostro sistema l'1 ha valore a seconda del posto che occupa nel numero
8/10 così l'1 può valere uno dieci cento mille ... e il 2 può valere due venti duecento duemila ...
9/10 vale di più l'1 o il 3? Dipende dalla posizione che occupa nel numero
10/10 il confronto si può fare con qualsiasi sistema additivo
valore posizionale
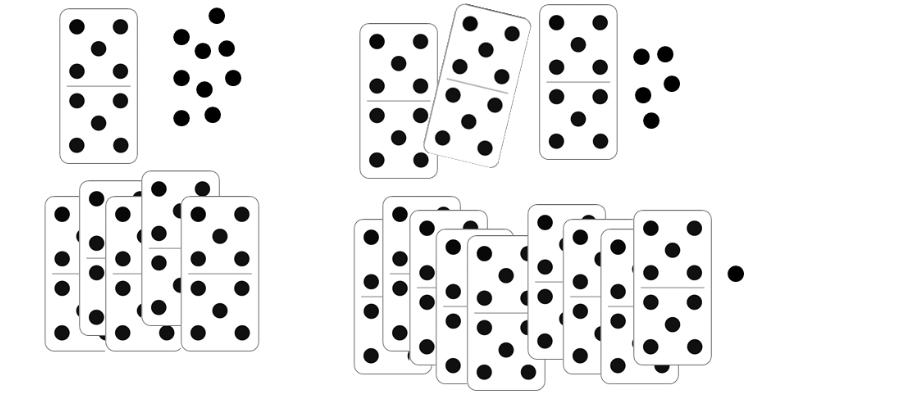
Insegnare e apprendere il valore posizionale delle cifre non è cosa semplice. Questo richiede tempo e attività varie e non basta una semplice “spiegazione”, per quanto ben fatta. Molte di queste attività possono essere svolte usando dei semplici cartellini dei numeri. Una cosa molto interessante che si può fare è il confronto tra un sistema di numerazione antico additivo con il nostro sistema di numerazione che è decimale.
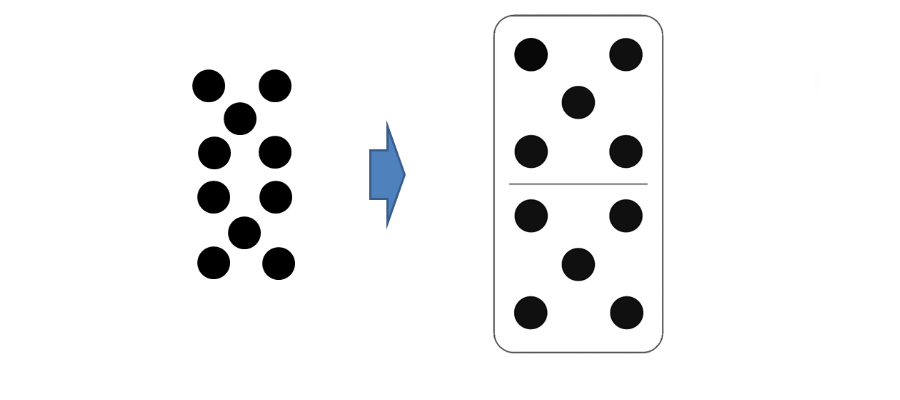
scomposizione di numeri
Ma come è fatto un numero? Siamo sicuri di riuscire a dare una risposta che sia esauriente per tutti a questa domanda? La costruzione del concetto di numero è una cosa complessa che si fa partecipando molte attività (il verbo alla forma transitiva è voluto = vivere attivamente un’esperienza). Tutti possiamo costruirci uno strumento che ci consente di crere e smontare numeri e di capire meglio come funzionano.
1/10 Per calcolare l'area si fa così ... applica la formula!
2/10 Ma siamo sicuri che con questo modo il bambino comprende realmente ciò che fa?
3/10 Proviamo in un altro modo. Quale oggetto occupa la superficie maggiore? E quanta superficie occupa?
4/10 Per sapere quanto è lunga una linea usiamo uno strumento ... ma esiste uno strumento analogo per le misure di superficie?
5/10 Eccolo: un foglio quadrettato
6/10 Ora abbiamo uno strumento per misurare, in quadretti, la superficie occupata da un oggetto
7/10 Ora possiamo capire e dire quanto misura
8/10 Possiamo esercitarci e misurare la superficie occupata da molti oggetti
9/10 Riflettiamo ... ma che quadretti sono questi? Sono quadretti da un centimetro, quindi ...
10/10 Ma per misurare la superficie occupata da una figurina serve proprio il quadrettato? O possiamo fare anche solo con il righello ...
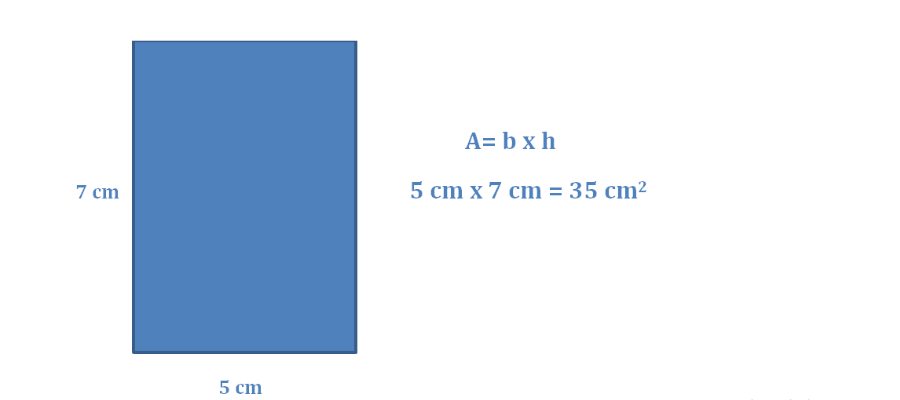
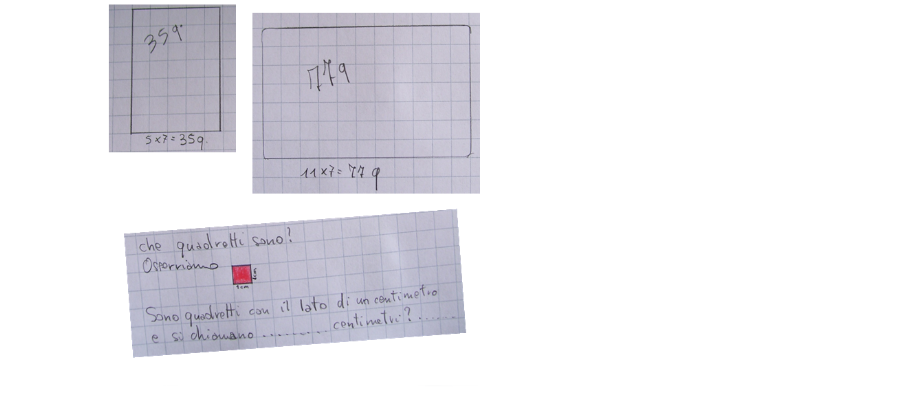
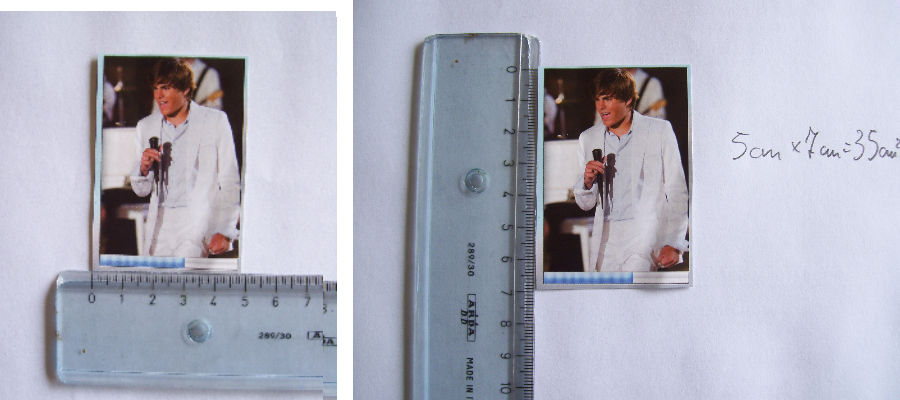
concetto di area
5 cm x 7 cm = 35 cm2 Dietro a questo semplice calcolo, c’è davvero una vera comprensione del concetto di area e del calcolo dell’area di una figura piana? Oppure c’è un automatismo senza comprensione? Qui trovi una risposta tanto semplice quanto efficace al “come costruire il concetto di calcolo dell’area?”
1/7 Un bollino e una tessera domino ci consentono di fare varie e interessanti attività su decine e unità e non solo
2/7 Le attività possono essere introdotte in vari modi ad esempio conteggiando i bollini che abbiamo preparato
3/7 Così presto si arriva all'esigenza di raggruppare per dieci che si conta meglio
4/7 E qui si può introdurre la tessera da dieci
5/7 Con tessere da dieci e bollini singoli si possono comporre i numeri
6/7 Ci si può esercitare in vari modi
7/7 Si possono creare le tessere per giocare, anche schede e altro per molti esercizi
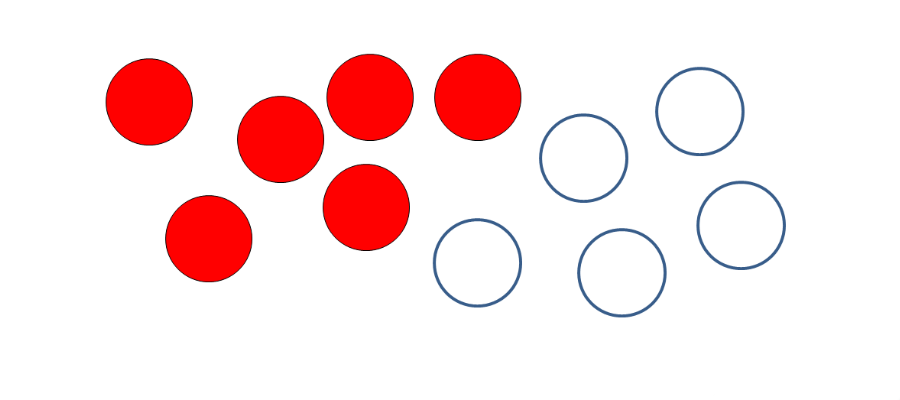
decine e unità
Quanto ci preoccupiamo nella restituzione di un compito ben fatto, che dietro ci sia comprensione e non solo un meccanismo di risposta acquisito, che mostra la sua debolezza se si pone la domanda in altro contesto? Il concetto di decina e di unità impegna notevolmente, insegnanti e bambini, nel primo anno di scuola. Non è facile insegnare a tutti e non è facile apprendere per tutti questo concetto senza uscire dal meccanicismo cui si è accennato poco sopra. Ma lo si può fare con la partecipazione a varie attività. Questi oggetti ne suggeriscono alcune molto interessanti.
1/8 Possiamo creare tanti bollini colorati per giocare con i numeri e capirne il funzionamento
2/8 Tutto è molto semplice, creiamo i bollini con i bambini e poi proviamo a dare loro un valore in base al colore ma se si vuole anche alla grandezza se ne creiamo di diversa grandezza
3/8 E' semplice creare numeri con i bollini possiamo iniziare gradualmente
4/8 Creare numeri diventa un gioco
1/8 Procediamo sempre con gradualità
6/8 Facciamo cose sempre più difficili giocando
7/8 E se creiamo anche altri bollini, gialli ad esempio?
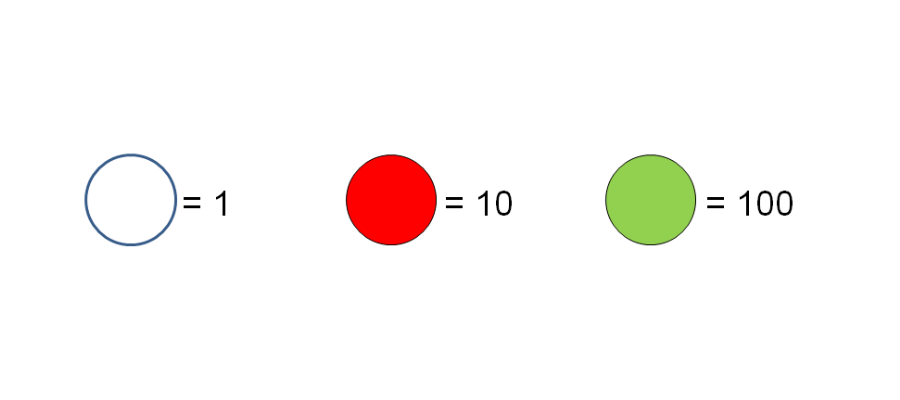
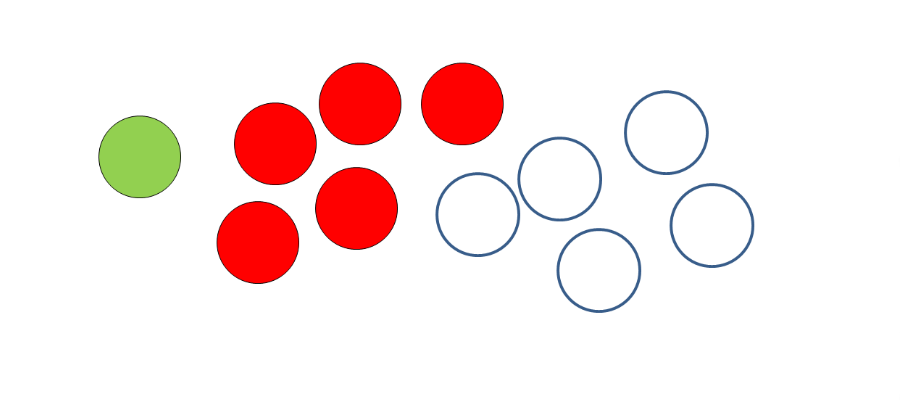
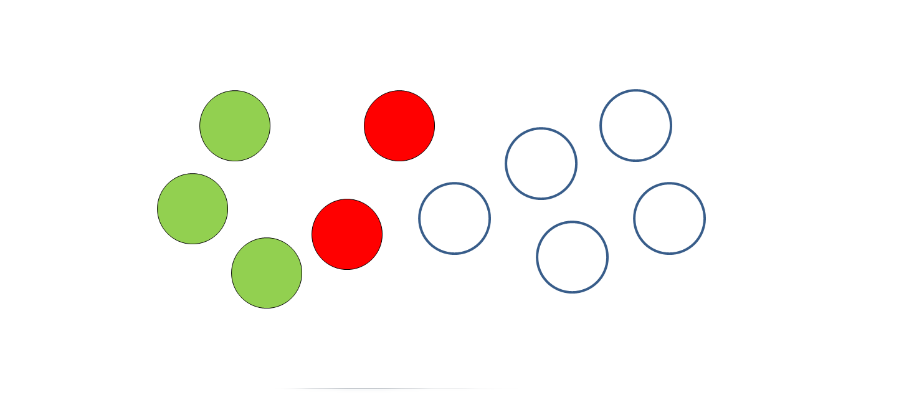
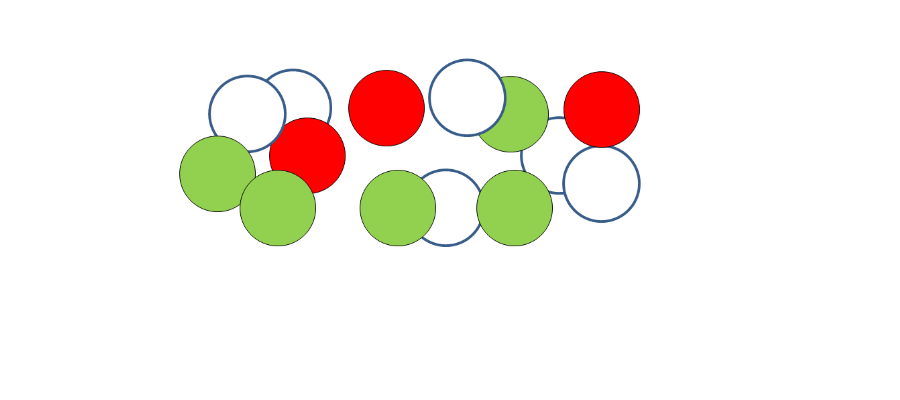
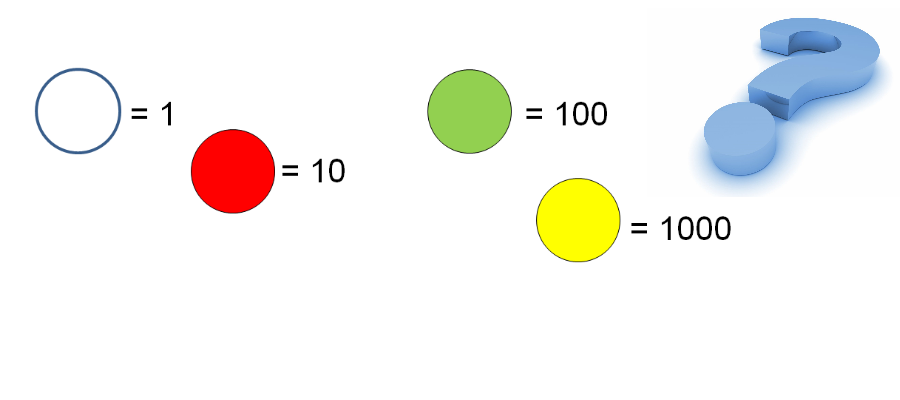
unità decine centinaia
Coltivare e sviluppare la comprensione di questi concetti sappiamo che non è facile. Spesso ci buttiamo in esercizi che per i bambini sono senza senso. Un fare ragionato per questo risulta sempre utile allo scopo di stimolare attività di pensiero positivo e non ripetitivo. Osserva e immagina quante altre attività puoi fare con questi oggetti.
1/6 Possiamo lavorare sul movimento di figure usando una figura in cartone, nastro carta e un pavimento
2/6 E' molto semplice muovere le figure lungo una linea seguendo un quadrettato
3/6
4/6 Riesce facile anche ribaltare una figura e parlare di simmetria
5/6
6/6 Come a l solito si fa si parla si riflette si verbalizza e si fa anche sul quaderno e ci si esercita
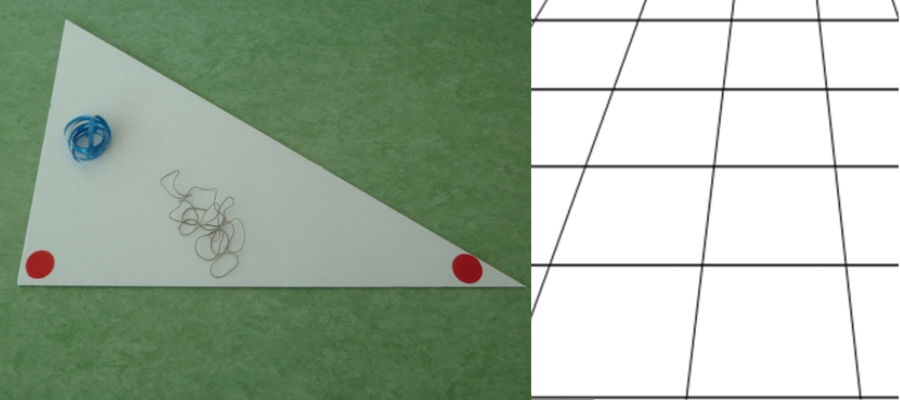
movimento di figure
Alle volte non ci accorgiamo di avere a disposizione degli strumenti semplici che ci consentono di fare attività molto interessanti. Un pavimento piastrellato può essere un quadrettato dove si fare, riflettere, capire e anche dare senso ad una terminologia difficile, come ad esempio vettore, ribaltamento, simmestria.Molti altri percorsi...
Materiali e attività sono presentati a titolo di esempio e di stimolo. Combinando le tue idee e la tua creatività con i materiali fisici e software che trovi nel sito, potrai creare in modo semplice molti altri percorsi che come questi ti consentiranno di proporre ai bambini esperienze cognitivamente dense e altamente efficaci.